Contents
Ejercicio 1
function fact=factr(n) if n==0 fact=1; else fact=n*factr(n-1); end end %apartado b function com=combina(n,i) com=factr(n)/(factr(i)*factr(n-i)); end %apartado c function bern=bernstein(t,n,i) bern=combina(n,i)*(t.^i).*((1-t).^(n-i)); end
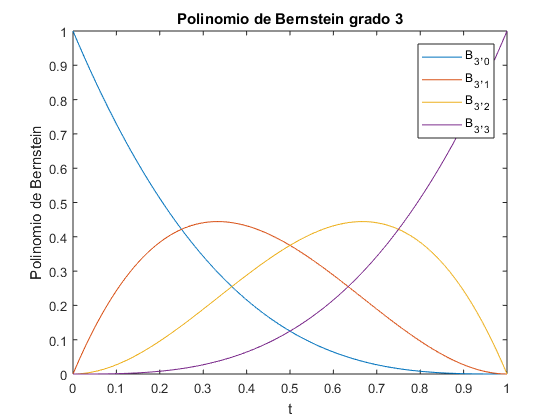
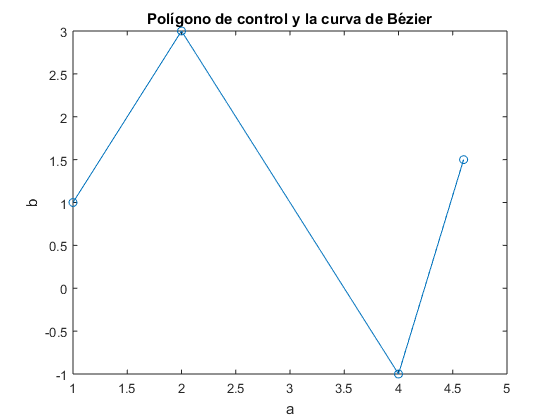
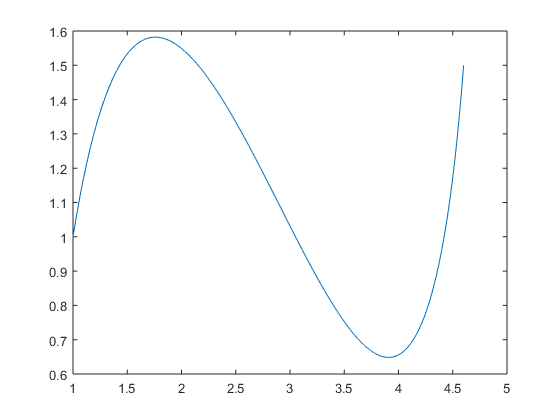
%apartado d t=linspace(0,1); n=3; figure(2) for i=0:n; plot(t,bernstein(t,n,i)); xlabel('t'); ylabel('Polinomio de Bernstein'); title('Polinomio de Bernstein grado 3'); legend('B_3,_0','B_3,_1','B_3,_2','B_3,_3'); hold on end %apartado e t=linspace(0,1); V=[1, 2, 4, 4.6;1, 3, -1, 1.5]; figure(1) plot(V(1,:),V(2,:),'-o');%grafico los puntos de control n=size(V); n=n(2); s=size(t); x=zeros(n,s(2)); y=zeros(n,s(2)); for i=1:n; x(i,:)=bernstein(t,n-1,i-1)*V(1,i); %separamos vector x y vector y y(i,:)=bernstein(t,n-1,i-1)*V(2,i); end a=sum(x); b=sum(y); xlabel('a');ylabel('b'); title('Polígono de control y la curva de Bézier'); hold on; figure(3) plot(a,b);
Warning: Ignoring extra legend entries. Warning: Ignoring extra legend entries. Warning: Ignoring extra legend entries.
Ejercicio 2
%apartado a z=xlsread('sotaventogaliciaanual.xlsx'); nbins=linspace(0,25); plot(z);figure;hist(z,nbins)
Ejercicio3
function x=funcionmuelle(t,x,c) x=[x(2);(-c*x(2)-20*x(1))/20]; end function solucion [t1,x1]=ode45(@funcionmuelle,[0,40],[1,0],[ ],5); plot(t1,x1(:,1)) hold on [t2,x2]=ode45(@funcionmuelle,[0,40],[1,0],[ ],40); plot(t2,x2(:,1)) [t3,x3]=ode45(@funcionmuelle,[0,40],[1,0],[ ],200); plot(t3,x3(:,1)) end